문제
프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제 설명
문제 요약: 택시 같이 타서 아끼는 비용 계산해서 합승 제안하기
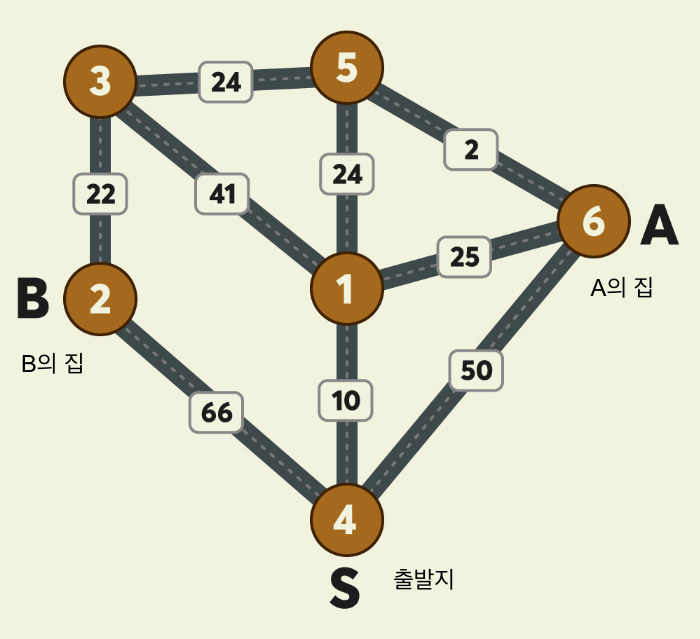
- 그림의 원은 지점을 나타내며 원 안의 숫자는 지점 번호를 나타냄
- 지점이 n개일 때, 지점 번호는 1부터 n까지 사용
- 지점 간에 택시가 이동할 수 있는 경로를 간선이라 하며, 간선에 표시된 숫자는 두 지점 사이의 예상 택시요금을 나타냄
- 간선은 편의 상 직선으로 표시
- 위 그림 예시에서, 4번 지점에서 1번 지점으로(4→1) 가거나, 1번 지점에서 4번 지점으로(1→4) 갈 때 예상 택시요금은 10원으로 동일
예상되는 최저 택시요금
- 4→1→5 : A, B가 합승하여 택시를 이용합니다. 예상 택시요금은 10 + 24 = 34원
- 5→6 : A가 혼자 택시를 이용합니다. 예상 택시요금은 2원
- 5→3→2 : B가 혼자 택시를 이용합니다. 예상 택시요금은 24 + 22 = 46원
- A, B 모두 귀가 완료까지 예상되는 최저 택시요금은 34 + 2 + 46 = 82원

n: 지점의 개수
s: 출발지점
a: a의 도착지점
b: b의 도착지점
fares: 지점 사이의 예상 택시요금
result: 최저 예상 택시 요금
접근
이 코드는 주어진 지점 간의 최소 비용을 구하는 문제임
출발지에서 각 지점까지의 최단 거리를 구하는 것이 아니라, 출발지에서 A와 B로의 최단 거리 합이 가장 작은 값을 구하는 문제임
따라서, 출발지에서 각 지점까지의 최단 거리를 구한 후에도 최단 거리의 합이 아닌 A와 B로의 최단 거리 합을 계산해야 함
다익스트라 알고리즘을 사용하여 최단 경로를 찾기
- preprocess 함수는 입력으로 받은 fares 리스트를 기반으로 그래프를 생성
- n개의 노드를 가지는 그래프를 생성한 후, fares에 있는 각 간선 정보를 그래프에 추가양방향 그래프이므로 간선은 양쪽으로 추가)
- dijkstra 함수는 주어진 그래프와 시작 노드(src)와 도착 노드(dst)를 입력으로 받아 최단 거리를 계산
- 모든 노드의 거리를 무한대(INF)로 초기화한 후, 시작 노드의 거리를 0으로 설정
- 우선순위 큐(pq)를 사용하여 방문할 노드를 관리
- 우선순위 큐에서 가장 짧은 거리의 노드를 꺼내면서 해당 노드와 연결된 인접 노드들을 확인
- 현재 노드를 거쳐 인접 노드로 가는 거리(new_distance)를 계산하고, 만약 이 거리가 인접 노드까지의 현재 최단 거리보다 작다면 거리를 갱신하고 우선순위 큐에 새로운 거리와 노드를 추가
- 우선순위 큐가 빌 때까지 반복
- solution 함수는 주어진 입력에 따라 최소 비용을 계산
- 출발지(s)에서 A(a)와 B(b)로의 최단 거리 합을 계산
- 모든 노드(i)에 대해 출발지에서 i로 이동한 후, i에서 A와 B로의 최단 거리 합을 계산하여 최솟값을 갱신
- 최종적으로 계산된 최소 비용을 반환
코드
from heapq import heappop, heappush
INF = int(1e9)
def preprocess(n, fares):
# 그래프 초기화
graph = [[] for _ in range(n + 1)]
# 주어진 fares를 기반으로 그래프 생성
for fare in fares:
src, dst, cost = fare[0], fare[1], fare[2]
# 양방향 그래프이므로 양쪽으로 간선 추가
graph[src].append([dst, cost])
graph[dst].append([src, cost])
return graph
def dijkstra(graph, src, dst):
n = len(graph)
distance = [INF] * n
distance[src] = 0
pq = [(0, src)] # 우선순위 큐를 사용하여 노드를 방문할 때마다 가장 짧은 거리 순서대로 방문
while pq:
w, x = heappop(pq) # 우선순위 큐에서 가장 짧은 거리의 노드를 꺼냄
if distance[x] < w:
continue
for neighbor, weight in graph[x]: # 현재 노드와 연결된 인접 노드를 확인
new_distance = weight + w # 현재 노드를 거쳐 인접 노드로 가는 거리 계산
if new_distance < distance[neighbor]: # 더 짧은 거리를 찾은 경우
distance[neighbor] = new_distance # 거리 갱신
heappush(pq, (new_distance, neighbor)) # 우선순위 큐에 새로운 거리와 노드를 추가
return distance[dst] # 시작 노드로부터 목적지 노드까지의 최단 거리 반환
def solution(n, s, a, b, fares):
graph = preprocess(n, fares) # 그래프 생성
cost = dijkstra(graph, s, a) + dijkstra(graph, s, b) # 출발지에서 A와 B로의 최단 거리 합 계산
for i in range(1, n + 1):
if s != i:
# 출발지에서 i로 이동한 후, i에서 A와 B로의 최단 거리 합 계산하여 최솟값 갱신
cost = min(cost, dijkstra(graph, s, i) + dijkstra(graph, i, a) + dijkstra(graph, i, b))
return cost # 최소 비용 반환'프로그래밍 > 알고리즘' 카테고리의 다른 글
| 프로그래머스 - 경주로 건설 파이썬 (0) | 2023.06.26 |
|---|---|
| 프로그래머스 - 이모티콘 할인행사 파이썬 (0) | 2023.06.22 |
| 백준 1302 - 베스트셀러 파이썬 (0) | 2023.06.16 |
| 냅색(Knapsack)알고리즘(배낭 문제) (0) | 2023.06.14 |
| 백준 14225 - 부분수열의 합 (0) | 2023.06.13 |




댓글