문제

프로그래머스
코드 중심의 개발자 채용. 스택 기반의 포지션 매칭. 프로그래머스의 개발자 맞춤형 프로필을 등록하고, 나와 기술 궁합이 잘 맞는 기업들을 매칭 받으세요.
programmers.co.kr
문제정리
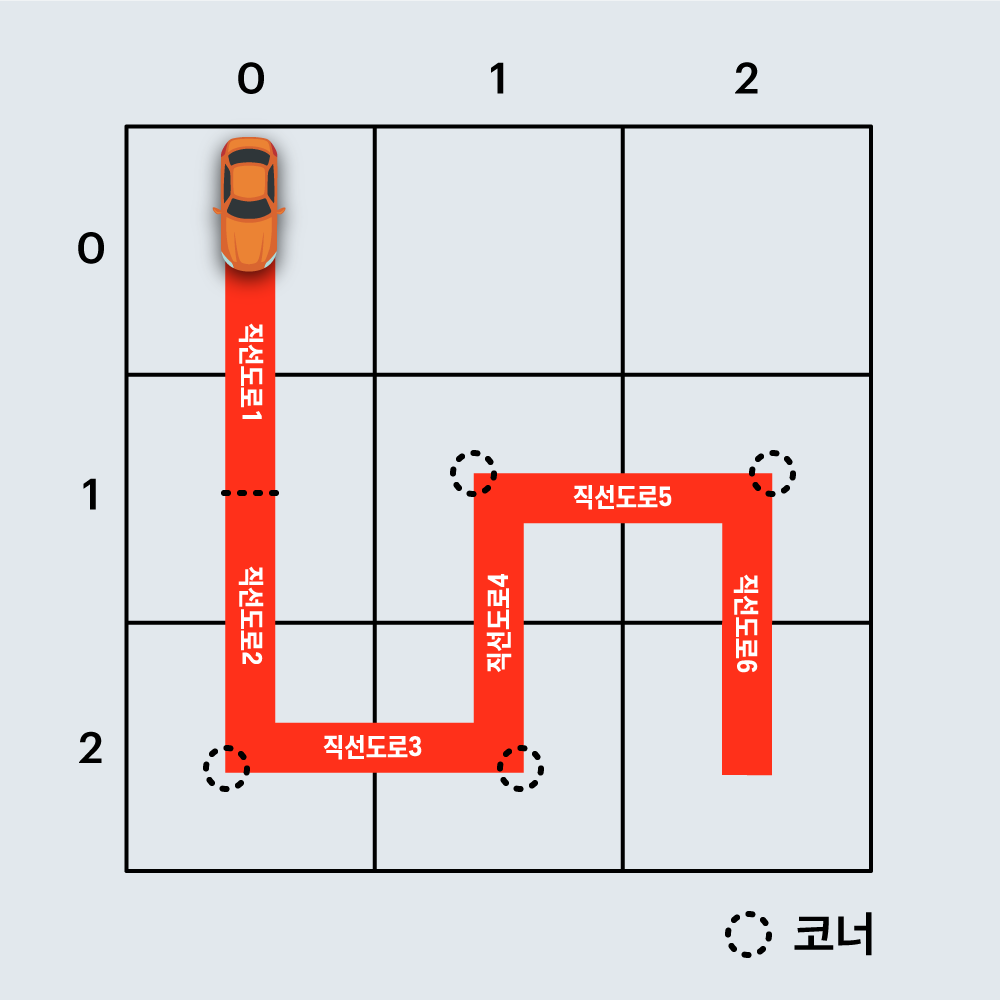
- 건설회사인 죠르디는 고객사로부터 자동차 경주로 건설 견적 의뢰를 받음
- 설계도면의 각 격자의 칸은 0또는 1로 채워져 있으며, 0은 비었음을 1은 채워있음을 나타냄
- 출발점인 (0, 0)칸에서 도착점인 (n-1, n-1)칸까지 무사히 도달할 수 있게 중간에 안끊기게 건설
- 직선도로: 인접한 두 빈칸을 상하또는 좌우로 연결한 경주로, 설치시 100원 소요
- 코너: 직선 도로가 서로 직각으로 만나는 지점 , 설치시 500원 소요
- 경주로 건설하는 최소 비용을 계산해야 함
예시 추가
board: 도면의 상태를 나타내는 2차원 배열
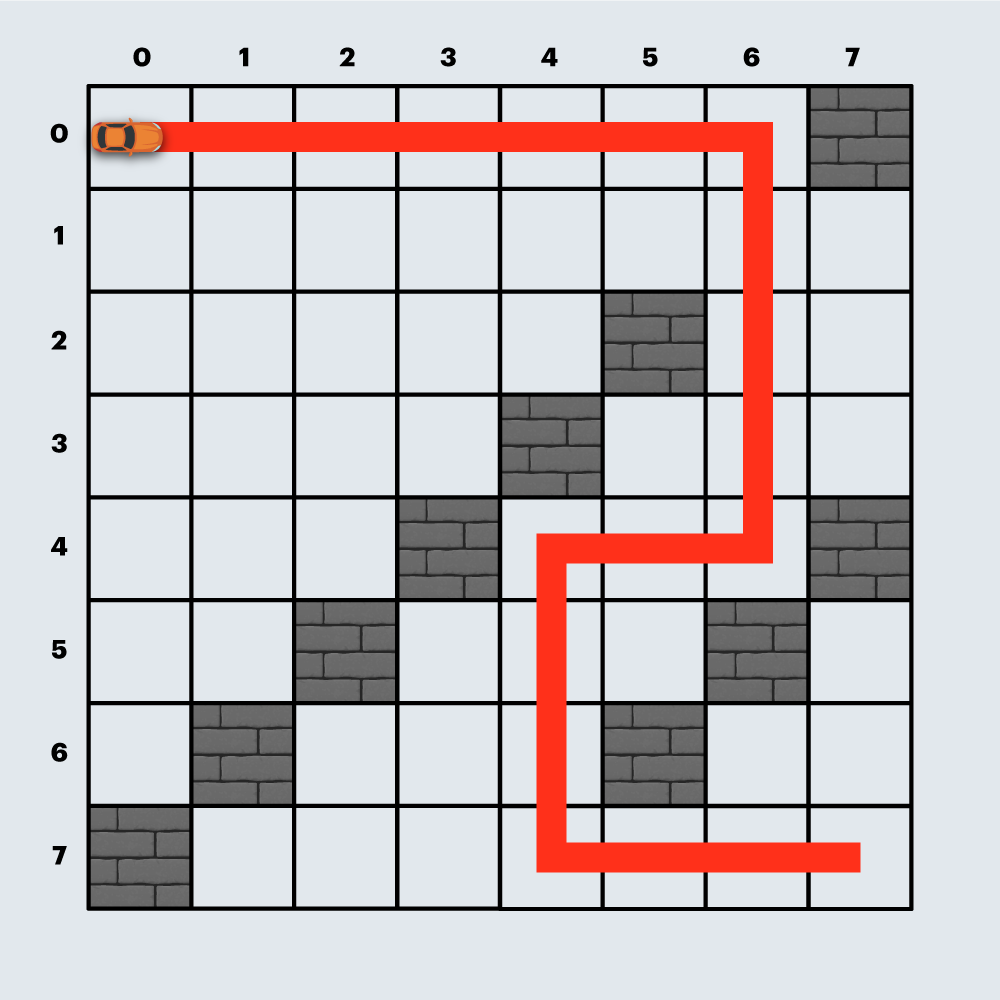
board: [[0,0,0,0,0,0,0,1],[0,0,0,0,0,0,0,0],[0,0,0,0,0,1,0,0],[0,0,0,0,1,0,0,0],[0,0,0,1,0,0,0,1],[0,0,1,0,0,0,1,0],[0,1,0,0,0,1,0,0],[1,0,0,0,0,0,0,0]]
board: [[0,0,1,0],[0,0,0,0],[0,1,0,1],[1,0,0,0]]

board: [[0,0,0,0,0,0],[0,1,1,1,1,0],[0,0,1,0,0,0],[1,0,0,1,0,1],[0,1,0,0,0,1],[0,0,0,0,0,0]]
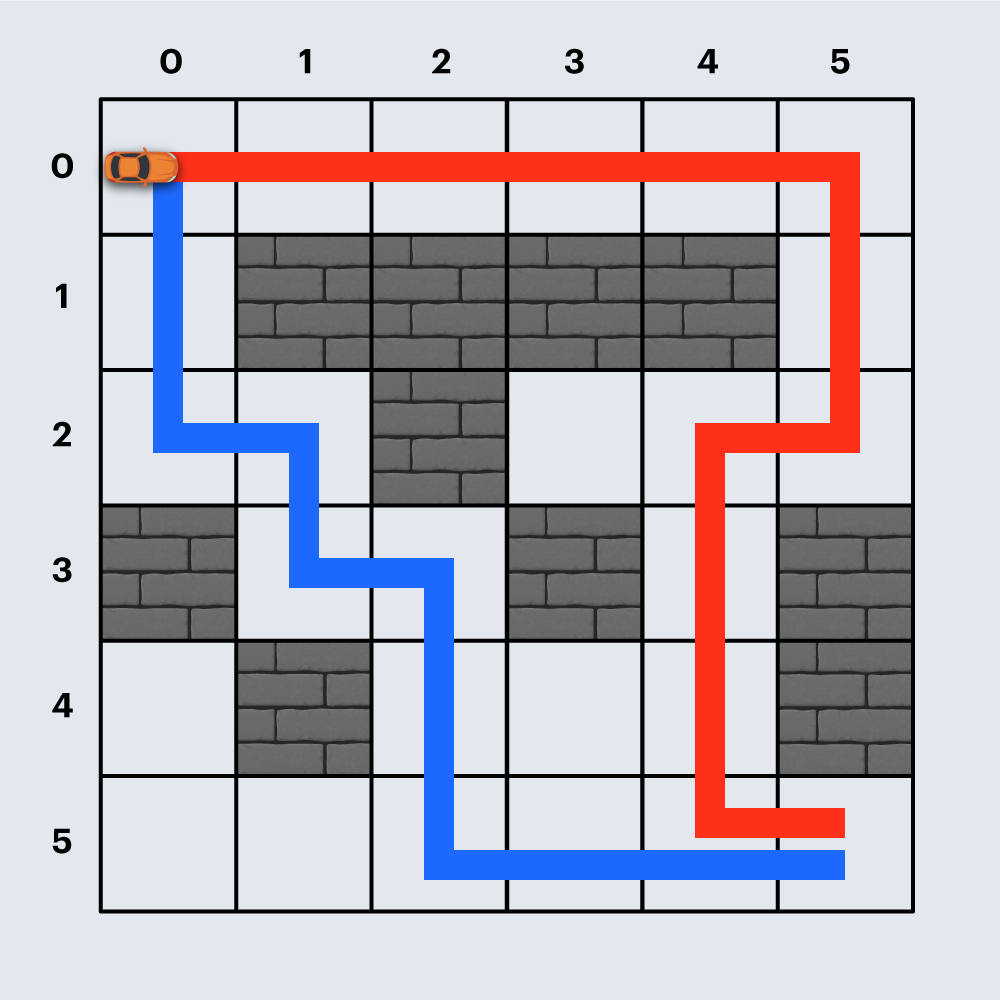
무슨 알고리즘을 쓸까
최단거리를 묻는 문제이므로 시작점에서 오른쪽 방향, 아래방향으로 두 가지 케이스로 나누어서 bfs를 적용
해결 코드
from collections import deque
import math
dx, dy = [0, 0, 1, -1], [1, -1, 0, 0]
def solution(board):
def bfs(start_x, start_y, start_cost, start_direction):
n = len(board)
result = [[math.inf for _ in range(n)] for _ in range(n)] # 최소 비용을 저장하는 배열 초기화
queue = deque()
queue.append((start_x, start_y, start_cost, start_direction)) # 시작 위치와 비용, 진행 방향을 큐에 추가
result[start_x][start_y] = 0 # 시작 위치의 비용을 0으로 설정
while queue:
x, y, cost, direction = queue.popleft()
for i in range(4): # 상하좌우 네 방향 탐색
new_x, new_y, new_cost = x + dx[i], y + dy[i], cost + 600 if i != direction else cost + 100
if 0 <= new_x < n and 0 <= new_y < n and board[new_x][new_y] == 0 and result[new_x][new_y] > new_cost:
# 이동한 위치가 범위 내에 있고, 벽이 아니며, 새로운 비용이 현재 비용보다 작을 경우
result[new_x][new_y] = new_cost # 최소 비용 업데이트
queue.append((new_x, new_y, new_cost, i)) # 큐에 새로운 위치와 비용, 진행 방향 추가
return result[-1][-1] # 마지막 위치의 최소 비용 반환
return min(bfs(0, 0, 0, 0), bfs(0, 0, 0, 2)) # 시작 위치로부터 진행 방향이 오른쪽인 경우와 아래쪽인 경우 중 최소 비용 반환- 완전탐색을 하기 위해 (x좌표, y좌표, 비용, 방향)정보를 바탕으로 진행
- 방향이 필요한 이유는 직선과 코너를 판별해주기 위함
- 'bfs(0, 0, 0, 2)'는 좌측 상단에서 오른쪽으로 가는 경우, 'bfs(0, 0, 0, 0)'는 좌측 상단에서 아래로 가는 경우
- 직선은 100원, 코너는 600원으로 계산(코너경로+직선경로를 건설한 것일 것이기 때문)
- 시간복잡도는 O(N*2)
'프로그래밍 > 알고리즘' 카테고리의 다른 글
| 프로그래머스 - 입국심사 파이썬 (0) | 2023.07.10 |
|---|---|
| 프로그래머스 - 징검다리 건너기 파이썬 (0) | 2023.07.03 |
| 프로그래머스 - 이모티콘 할인행사 파이썬 (0) | 2023.06.22 |
| 프로그래머스 - 합승 택시 요금 파이썬 (0) | 2023.06.20 |
| 백준 1302 - 베스트셀러 파이썬 (0) | 2023.06.16 |




댓글